题目内容
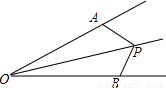
如图，已知∠AOP=∠BOP，PC∥OA，PD⊥OA，若∠OPD=75°，则∠BCP等于
- A.15°
- B.30°
- C.35°
- D.75°
B
分析：由两直线平行，同位角相等可以得出∠BCP=∠BOA=∠BOP+∠AOP，又∠AOP=∠BOP，故可得出：∠BCP=2∠AOP，只要求出∠AOP的值，即可求出∠BCP的值，已知∠OPD=75°，PD⊥OA，所以∠AOP=90°-∠OPD．
解答：∵PC∥OA，
∴∠BCP=∠BOA=∠BOP+∠AOP，
又∵∠AOP=∠BOP，
∴∠BCP=2∠AOP；
在Rt△OPD中，PD⊥OA，∠OPD=75°，
∠AOP=90°-∠OPD=90°-75°=15°，
∴∠BCP=2∠AOP=30°．
故选：B．
点评：本题主要考查了平行线的性质：两直线平行，同位角相等．利用该性质求出未知角与已知角的关系，进而求出该未知角．
分析：由两直线平行，同位角相等可以得出∠BCP=∠BOA=∠BOP+∠AOP，又∠AOP=∠BOP，故可得出：∠BCP=2∠AOP，只要求出∠AOP的值，即可求出∠BCP的值，已知∠OPD=75°，PD⊥OA，所以∠AOP=90°-∠OPD．
解答：∵PC∥OA，
∴∠BCP=∠BOA=∠BOP+∠AOP，
又∵∠AOP=∠BOP，
∴∠BCP=2∠AOP；
在Rt△OPD中，PD⊥OA，∠OPD=75°，
∠AOP=90°-∠OPD=90°-75°=15°，
∴∠BCP=2∠AOP=30°．
故选：B．
点评：本题主要考查了平行线的性质：两直线平行，同位角相等．利用该性质求出未知角与已知角的关系，进而求出该未知角．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
10、如图，已知∠AOP=∠BOP，PC∥OA，PD⊥OA，若∠OPD=75°，则∠BCP等于（ ）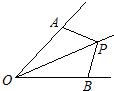
8、如图，已知∠AOP=∠BOP，若使△AOP≌△BOP，则下列需添加的一个条件不正确的是（ ）
