题目内容
【题目】已知 AB 为⊙O 的直径,BC⊥AB 于 B,且 BC=AB,D 为半圆⊙O 上的一点,连接 BD 并延长交半圆⊙O 的切线 AE 于 E.

(1)如图 1,若 CD=CB,求证:CD 是⊙O 的切线;
(2)如图 2,若 F 点在 OB 上,且CD⊥DF,求![]() 的值.
的值.
【答案】(1)①不可能;②见解析;(2)![]()
【解析】
(1)连接DO,CO,易证△CDO≌△CBO,即可解题;
(2)连接AD,易证△ADF∽△BDC和△ADE∽△BDA,根据相似三角形对应边成比例的性质即可解题.
(1)连接DO,CO,
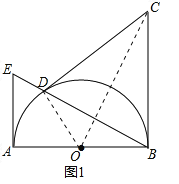
∵BC⊥AB于B,
∴∠ABC=90°,
在△CDO与△CBO中,
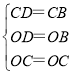 ,
,
∴△CDO≌△CBO,
∴∠CDO=∠CBO=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)连接AD,
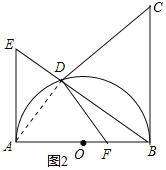
∵AB是直径,∴∠ADB=90°,
∴∠ADF+∠BDF=90°,∠DAB+∠DBA=90°,
∵∠BDF+∠BDC=90°,∠CBD+∠DBA=90°,
∴∠ADF=∠BDC,∠DAB=∠CBD,
∵在△ADF和△BDC中,
![]() ,
,
∴△ADF∽△BDC,
∴![]() ,
,
∵∠DAE+∠DAB=90°,∠E+∠DAE=90°,
∴∠E=∠DAB,
∵在△ADE和△BDA中,
![]() ,
,
∴△ADE∽△BDA,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵AB=BC,
∴![]() =1.
=1.

 课课通课程标准思维方法与能力训练系列答案
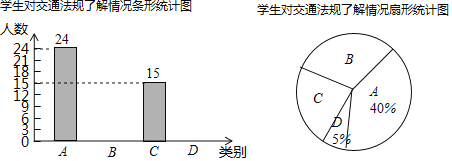
课课通课程标准思维方法与能力训练系列答案【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?