题目内容
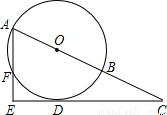
已知,如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边三角形。
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形。
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形。

证明:(1)∵BF=AC,AB=AE,
∴FA=EC,
∵△DEF是等边三角形,
∴EF=DE,
又∵AE=CD(已知),
∴△AEF≌△CDE(SSS);
(2)由△AEF≌△CDE,得∠FEA=∠EDC,
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
△DEF是等边三角形,
∴∠DEF=60°,
∴∠BCA=60°,同理可得∠BAC=60°,
∴△ABC中,AB=BC,
∴△ABC是等边三角形。
∴FA=EC,
∵△DEF是等边三角形,
∴EF=DE,
又∵AE=CD(已知),
∴△AEF≌△CDE(SSS);
(2)由△AEF≌△CDE,得∠FEA=∠EDC,
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
△DEF是等边三角形,
∴∠DEF=60°,
∴∠BCA=60°,同理可得∠BAC=60°,
∴△ABC中,AB=BC,
∴△ABC是等边三角形。

练习册系列答案
相关题目
 21、已知,如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边三角形.
21、已知,如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边三角形.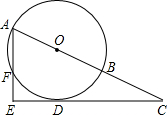 O于点F,垂足为点E,连接AD.
O于点F,垂足为点E,连接AD.