题目内容
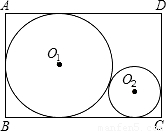
(2000•昆明)工厂有一批长24cm,宽16cm的矩形铁片,在每一块上截下一个最大的圆铁片⊙O1之后,再在剩余铁片上截下一个充分大的圆铁片⊙O2,如图.(1)求⊙O1与⊙O2的半径R、r的长;
(2)能否在第二次剩余铁片上再截出一个与⊙O2同样大小的圆铁片,为什么?
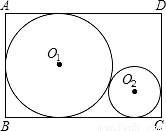
【答案】分析:(1)显然⊙O1的直径等于矩形的宽,即16,则R=8;连接两圆的圆心和各个切点,组成一个直角梯形,作梯形的另一高,组成直角三角形,根据勾股定理列方程计算;
(2)根据2r大于铁皮宽(16cm)的一半可知,不能再截出一个与⊙O2同样大小的圆铁片.
解答: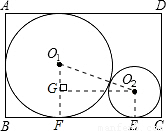 解:(1)显然⊙O1的半径是矩形ABCD的宽的一半,即8.
解:(1)显然⊙O1的半径是矩形ABCD的宽的一半,即8.
设两圆和BC分别切于点F,E,连接O1O2,O1F、O2E,得到一个直角梯形,作梯形的另一高.
根据在Rt△GO1O2中,由勾股定理,得:
(8+r)2=(8-r)2+(24-8-r)2,
r1=32-16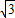 ,r2=32+16
,r2=32+16 (不合题意舍去).
(不合题意舍去).
(2)因为2r>8,所以剩余铁皮的宽小于8,所以无法截出一个与⊙O2同样大小的圆铁片.
点评:能够构造一个直角三角形,根据勾股定理列方程进行求解.
(2)根据2r大于铁皮宽(16cm)的一半可知,不能再截出一个与⊙O2同样大小的圆铁片.
解答:
 解:(1)显然⊙O1的半径是矩形ABCD的宽的一半,即8.
解:(1)显然⊙O1的半径是矩形ABCD的宽的一半,即8.设两圆和BC分别切于点F,E,连接O1O2,O1F、O2E,得到一个直角梯形,作梯形的另一高.
根据在Rt△GO1O2中,由勾股定理,得:
(8+r)2=(8-r)2+(24-8-r)2,
r1=32-16
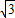 ,r2=32+16
,r2=32+16 (不合题意舍去).
(不合题意舍去).(2)因为2r>8,所以剩余铁皮的宽小于8,所以无法截出一个与⊙O2同样大小的圆铁片.
点评:能够构造一个直角三角形,根据勾股定理列方程进行求解.

练习册系列答案
相关题目