题目内容
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”给出下列定义: 若
的“非常距离”给出下列定义: 若![]() ,则点
,则点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() . 例如:点
. 例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与
与![]() 的“非常距离”为
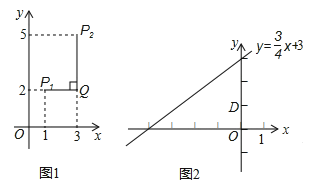
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点Q为垂直于
长度的较大值(点Q为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点A![]() ,B为
,B为![]() 轴上一个动点.
轴上一个动点.
①若点B(0,3),则点A与点B的“非常距离”为 ;
②若点A与点B的“非常距离”为2,则点B的坐标为 ;
③直接写出点A与点B的“非常距离”的最小值 .
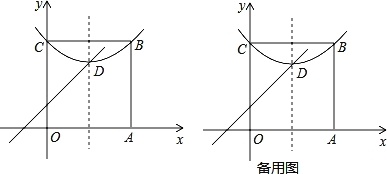
(2)已知点D(0,1)点C是直线![]() 上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
【答案】(1)①3,②(0,2)或(0,-2) ③![]() (2)
(2)![]()
【解析】试题分析:(1)①根据若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|解答即可;
②根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0-y|=2,据此可以求得y的值;
③设点B的坐标为(0,y).因为|-![]() -0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-
-0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-![]() -0|=
-0|=![]() ;
;
(2)设点C的坐标为(x0, ![]() x0+3).根据材料“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”知,C、D两点的“非常距离”的最小值为-x0=
x0+3).根据材料“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”知,C、D两点的“非常距离”的最小值为-x0=![]() x0+2,据此可以求得点C的坐标.
x0+2,据此可以求得点C的坐标.
试题解析:(1)∵|-![]() -0|=
-0|=![]() ,|0-3|=3,
,|0-3|=3,
∴![]() <3,
<3,
∴点A与点B的“非常距离”为3.
②∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|-![]() -0|=
-0|=![]() ≠2,
≠2,
∴|0-y|=2,
解得,y=2或y=-2;
∴点B的坐标是(0,2)或(0,-2),
③点A与点B的“非常距离”的最小值为![]() .
.
(2)如图2,取点C与点D的“非常距离”的最小值时,

需要根据运算定义“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”解答,
此时|x1-x2|=|y1-y2|,即AC=AD,
∵C是直线y=![]() x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0, ![]() x0+3),
x0+3),
∴-x0=![]() x0+2,
x0+2,
此时,x0=-![]() ,
,
∴点C与点D的“非常距离”的最小值为:|x0|=![]() ,
,
此时C(-![]() ,
, ![]() ).
).