题目内容
等腰三角形的底边长为20，有一个内角为30°，求底边上的高．分析：本题中要注意说明了内角为30°，但并未说明是顶角还是底角，因此要分情况讨论．
解答：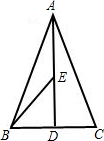
解：分两种情况讨论：
（1）底角为30°，设底边上的高为x，得出4x2=x2+102，解方程得x=
；
（2）顶角为30°，那么底角就是75°，如图，在底边上的高AD上取一点E使AE=EB，那么
∠BAE=∠EBA=15°，∠BED=30°，BD=10，
因此DE=BD•tan60°=10
，
BE=BD÷sin30°=20
因此，AD=AE+DE=BE+DE=20+10
答：底边上的高是
或20+10
．
解：分两种情况讨论：（1）底角为30°，设底边上的高为x，得出4x2=x2+102，解方程得x=
10
| ||
| 3 |
（2）顶角为30°，那么底角就是75°，如图，在底边上的高AD上取一点E使AE=EB，那么
∠BAE=∠EBA=15°，∠BED=30°，BD=10，
因此DE=BD•tan60°=10
| 3 |
BE=BD÷sin30°=20
因此，AD=AE+DE=BE+DE=20+10
| 3 |
答：底边上的高是
10
| ||
| 3 |
| 3 |
点评：本题中要分两种情况进行讨论，要注意当顶角为30°时，可通过作辅助线，把所求线段转换到含特殊角的直角三角形中进行计算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目