题目内容
一个直角三角形两条直角边为a=6,b=8,分别以它的两条直角边所在直线为轴,旋转一周,得到两个几何体,它们的表面面积相应地记为Sa 和 Sb,则有( )
| A.Sa = Sb | B.Sa < Sb | C.Sa > Sb | D.不确定 |
C
表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2,代入相应的数值计算比较即可.
解:根据题意,由勾股定理得,斜边=10,
∴以a=6为直角边的表面面积Sa=64π+80π=144π;
以b=8为直角边的表面面积Sb=36π+60π=96π,
∴Sa>Sb,
故选C.
本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
解:根据题意,由勾股定理得,斜边=10,
∴以a=6为直角边的表面面积Sa=64π+80π=144π;
以b=8为直角边的表面面积Sb=36π+60π=96π,
∴Sa>Sb,
故选C.
本题利用了勾股定理,圆的周长公式和扇形面积公式求解.

练习册系列答案
相关题目
 .
.


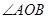 的边OB上的一点
的边OB上的一点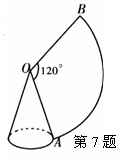
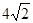 cm B.
cm B.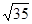 cm C.
cm C.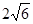 cm D.
cm D.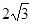 cm
cm