题目内容
如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.
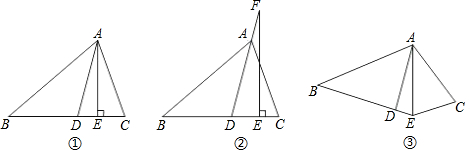
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.

分析:(1)求出∠ADE的度数,利用∠DAE=90°-∠ADE即可求出∠DAE的度数.
(2)求出∠ADE的度数,利用∠DFE=90°-∠ADE即可求出∠DAE的度数.
(3)利用AE平分∠BEC,AD平分∠BAC,求出∠DFE=15°即是最好的证明.
(2)求出∠ADE的度数,利用∠DFE=90°-∠ADE即可求出∠DAE的度数.
(3)利用AE平分∠BEC,AD平分∠BAC,求出∠DFE=15°即是最好的证明.
解答:解:(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°.
(2)同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
(3)结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD-∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD-∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C-∠B=30°,
∴∠DAE=15°.
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°.
(2)同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
(3)结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD-∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD-∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C-∠B=30°,
∴∠DAE=15°.
点评:本题考查了三角形内角和定理和三角形外角的性质,是一道好题.

练习册系列答案
相关题目
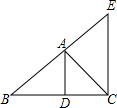 如图:若AD平分∠BAC,AD∥EC,则( )是等腰三角形.
如图:若AD平分∠BAC,AD∥EC,则( )是等腰三角形.| A、△ABD | B、△ACD | C、△ACE | D、△ABC |



