题目内容
(2005•浙江)如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.记CD的长为t.(1)当t=
 时,求直线DE的函数表达式;
时,求直线DE的函数表达式;(2)如果记梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由;
(3)当OD2+DE2的算术平方根取最小值时,求点E的坐标.
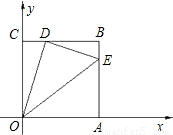
【答案】分析:(1)因为∠ODC+∠EDB=∠ODC+∠COD=90°,可得出∠DOC=∠EDB,同理得∠ODC=∠DEB,又因为∠OCD=∠B=90°,因此△CDO∽△BED,那么可得出关于OC,CD,BD,BE比例关系的式子,有CD的长,有OC,BC的长,那么可得出BE的长,因此就能求出E的坐标,然后根据待定系数法求出过DE的函数的关系式;
(2)要求梯形COEB的面积就必须知道BE的长,同(1)的方法,我们可以用t表示出BE,那么就能用关于t的式子表示出S,然后根据函数的性质来判断S的最大值及相应的t的值.
(3)当OD2+DE2的算术平方根取最小值时OE就最小,OA为定值,因此此时AE最小,那么三角形AOE的面积就最小,此时梯形OEBC的面积最大,那么也就是说OE最小时梯形OEBC的面积最大,根据(2)我们知道梯形最大时t的值,由此可得出E的坐标.
解答:解:(1)∵∠ODC+∠EDB=∠ODC+∠COD=90°,
∴∠DOC=∠EDB,
同理得∠ODC=∠DEB,
∵∠OCD=∠B=90°,
∴△CDO∽△BED,
∴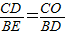 ,即
,即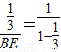 ,
,
得BE= ,则点E的坐标为E(1,
,则点E的坐标为E(1, ),
),
设直线DE的一次函数表达式为y=kx+b,直线经过两点D( ,1)和E(1,
,1)和E(1, ),
),
代入y=kx+b得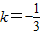 ,
, ,
,
故所求直线DE的函数表达式为y= ;
;
(2)存在S的最大值.
∵△COD∽△BDE,
∴ ,即
,即 ,BE=t-t2,
,BE=t-t2,
 ×1×(1+t-t2)=
×1×(1+t-t2)=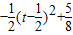 .
.
故当t= 时,S有最大值
时,S有最大值 ;
;
(3)在Rt△OED中,OD2+DE2=OE2,OD2+DE2的算术平方根取最小值,也就是斜边OE取最小值.
当斜边OE取最小值且一直角边OA为定值时,另一直角边AE达到最小值,
于是△OEA的面积达到最小值,
此时,梯形COEB的面积达到最大值.
由(2)知,当t= 时,梯形COEB的面积达到最大值,故所求点E的坐标是(1,
时,梯形COEB的面积达到最大值,故所求点E的坐标是(1, ).
).
点评:本题考查了正方形的性质,一次函数的综合应用以及相似三角形的性质等知识点.本题中用相似三角形得出比例关系,然后用线段的比例关系和CD表示出BE是解题的关键.
(2)要求梯形COEB的面积就必须知道BE的长,同(1)的方法,我们可以用t表示出BE,那么就能用关于t的式子表示出S,然后根据函数的性质来判断S的最大值及相应的t的值.
(3)当OD2+DE2的算术平方根取最小值时OE就最小,OA为定值,因此此时AE最小,那么三角形AOE的面积就最小,此时梯形OEBC的面积最大,那么也就是说OE最小时梯形OEBC的面积最大,根据(2)我们知道梯形最大时t的值,由此可得出E的坐标.
解答:解:(1)∵∠ODC+∠EDB=∠ODC+∠COD=90°,
∴∠DOC=∠EDB,
同理得∠ODC=∠DEB,
∵∠OCD=∠B=90°,
∴△CDO∽△BED,
∴
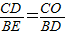 ,即
,即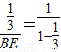 ,
,得BE=
 ,则点E的坐标为E(1,
,则点E的坐标为E(1, ),
),设直线DE的一次函数表达式为y=kx+b,直线经过两点D(
 ,1)和E(1,
,1)和E(1, ),
),代入y=kx+b得
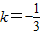 ,
, ,
,故所求直线DE的函数表达式为y=
 ;
;(2)存在S的最大值.
∵△COD∽△BDE,
∴
 ,即
,即 ,BE=t-t2,
,BE=t-t2, ×1×(1+t-t2)=
×1×(1+t-t2)=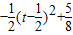 .
.故当t=
 时,S有最大值
时,S有最大值 ;
;(3)在Rt△OED中,OD2+DE2=OE2,OD2+DE2的算术平方根取最小值,也就是斜边OE取最小值.
当斜边OE取最小值且一直角边OA为定值时,另一直角边AE达到最小值,
于是△OEA的面积达到最小值,
此时,梯形COEB的面积达到最大值.
由(2)知,当t=
 时,梯形COEB的面积达到最大值,故所求点E的坐标是(1,
时,梯形COEB的面积达到最大值,故所求点E的坐标是(1, ).
).点评:本题考查了正方形的性质,一次函数的综合应用以及相似三角形的性质等知识点.本题中用相似三角形得出比例关系,然后用线段的比例关系和CD表示出BE是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目