题目内容
【题目】快、慢两车分别从相距480km路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1h,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路y km与所用时间x h之间的函数图象如图,请结合图象信息解答下列问题: 
(1)直接写出慢车的行驶速度和a的值;
(2)求快车的速度和B点坐标;
(3)快车与慢车第一次相遇时,距离甲地的路程是多少千米?
【答案】
(1)解:由题意,得
慢车的速度为:480÷(9﹣1)=60千米/时,
∴a=60×(7﹣1)=360千米.
答:慢车的行驶速度为60千米/时,a的值为360千米
(2)解:由题意,得:5×60=300,
∴D(5,300),设yOD=k1x,由题意,得300=5k1,
∴k1=60,
∴yOD=60x.
∵快车的速度为:(480+360)÷7=120千米/时.
∴480÷120=4小时.
∴B(4,0),C(8,480).
(3)解:设yAB=k2x+b,由题意,得:
![]() ,
,
解得: ![]() ,
,
∴yAB=﹣120x+480,
∴ ![]() ,
,
解得: 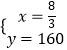 ,
,
∴480﹣160=320千米.
答:快车与慢车第一次相遇时,距离甲地的路程是320千米
【解析】(1)根据行程问题的数量关系:速度=路程÷时间及路程=速度×时间就可以得出结论;(2)由(1)的结论可以求出点D的坐标,再由题意可以求出快车的速度就可以求出点B的坐标.(3)由待定系数法求出AB的解析式及OD的解析式就可以求出结论.

练习册系列答案
相关题目