题目内容
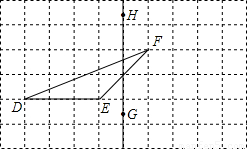
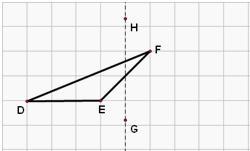21、认真画一画．如图，在正方形网格上有一个△DEF．（1）作△DEF关于直线HG的轴对称图形△D′E′F′（不写作法）；
（2）作EF边上的高（不写作法）；
（3）若网格上的最小正方形边长为1，则△DEF的面积为
3
．分析：（1）从三角形各边向HG引垂线并延长相同的长度，找到对应点，顺次连接；
（2）延长EF，从D点向延长线作垂线；
（3）根据网格找出三角形的底和高，利用面积公式计算．
（2）延长EF，从D点向延长线作垂线；
（3）根据网格找出三角形的底和高，利用面积公式计算．
解答：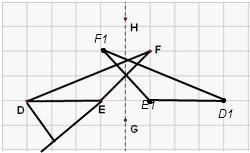
解：若网格上的最小正方形边长为1，
则可看出三角形的底是3，高是2，
所以△DEF的面积为3．（2分）
解：若网格上的最小正方形边长为1，则可看出三角形的底是3，高是2，
所以△DEF的面积为3．（2分）
点评：本题综合考查了轴对称图形及利用网格计算面积的能力．难度不大．
练习册系列答案
相关题目
21、认真画一画，培养你的作图能力．
认真画一画，培养你的作图能力．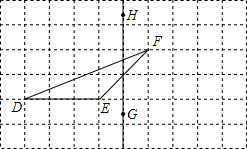
认真画一画．如图，在正方形网格上有一个△DEF．