Question

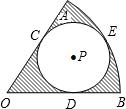如图，⊙P与扇形OAB的半径OA、OB分别相切于点C、D，与弧AB相切于点E，已知OA=15cm，∠AOB=60°，求图中阴影部分的面积．

Answer 1

分析：先求出⊙P的半径，再利用阴影部分面积=扇形的面积-圆的面积进行计算．

解答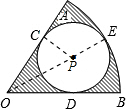：解：连接PC，OP，PE．
∵⊙P与扇形OAB的半径OA、OB分别相切于点C、D，
∴∠COP=

1

2

∠AOB=30°，∠OCP=90°，
在Rt△OPC中，
∵∠COP=30°，
∴OP=2PC，
∴2PC+PE=3PC=OE=OA=15，
∴⊙P的半径 PC=5．
∴S_⊙P=πr²=25π，
S_扇形=

60π×152

360

=

75π

2

，
∴S_阴=

75π

2

-25π=

25π

2

．
答：图中阴影部分的面积是

25π

2

．

点评：本题考查了相切两圆的性质．构造直角三角形是常用的方法，本题的关键是求得圆的半径．