题目内容
【题目】如图，直线AB，CD相交于点O，OE⊥CD于点O，∠EOB=115°，求∠AOC的度数．请补全下面的解题过程（括号中填写推理的依据）．
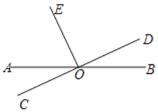
解：∵OE⊥CD于点O（已知），
∴______（______）．
∵∠EOB=115°（已知），
∴∠DOB=______=115°-90°=25°．
∵直线AB，CD相交于点O（已知），
∴∠AOC=______=25°（______）．
【答案】∠EOD=90°，垂直的定义，∠EOB-∠EOD，∠DOB，对顶角相等，见解析
【解析】
根据垂直的定义可得∠EOD=90°，根据角的和差关系可得∠DOB=∠EOB-∠EOD=115°-90°=25°，再根据对顶角的性质解答即可．
解：∵OE⊥CD于点O（已知），
∴∠EOD=90°（垂直的定义），
∵∠EOB=115°（已知），
∴∠DOB=∠EOB-∠EOD=115°-90°=25°．
∵直线AB，CD相交于点O（已知），
∴∠AOC=∠DOB=25°（对顶角相等）．
故答案为：∠EOD=90°；垂直的定义；∠EOB-∠EOD；∠DOB；对顶角相等．
练习册系列答案
相关题目
【题目】荣获“中华名果”称号的
市脐橙果大形正，橙红鲜艳，含果汁55%以上，深受广大“吃货”的喜爱．现有20筐市脐橙，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示,记录如下：
与标准质量的差值 （单位：千克） | -3 | -2 | -1．5 | 0 | 1 | 2．5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）在这20筐市脐橙中,最重的一筐比最轻的一筐重多少千克？
（2）与标准重量比较，20筐市脐橙总计超过或不足多少千克？
（3）若市脐橙每千克售价8元，则这20筐市脐橙可卖多少元？
