Question

【题目】已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．

（1）求证：AP=BQ；

（2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．

Answer 1

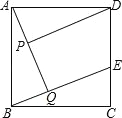
【答案】（1）证明见解析；（2）①AQ﹣AP=PQ，②AQ﹣BQ=PQ，③DP﹣AP=PQ，④DP﹣BQ=PQ.

【解析】

试题分析：（1）利用AAS证明△AQB≌△DPA，可得AP=BQ；（2）根据AQ﹣AP=PQ和全等三角形的对应边相等可写出4对线段.

试题解析：（1）在正方形中ABCD中，AD=BA，∠BAD=90°，∴∠BAQ+∠DAP=90°，∵DP⊥AQ，∴∠ADP+∠DAP=90°，∴∠BAQ=∠ADP，∵AQ⊥BE于点Q，DP⊥AQ于点P，∴∠AQB=∠DPA=90°，∴△AQB≌△DPA（AAS），

∴AP=BQ.（2）①AQ﹣AP=PQ，②AQ﹣BQ=PQ，③DP﹣AP=PQ，④DP﹣BQ=PQ.