题目内容
如图所示,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(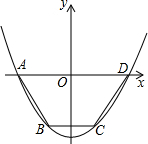 -2,0),B(-1,-3).
-2,0),B(-1,-3).(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A,B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标.
分析:(1)将A、B点的坐标代入抛物线的解析式中即可求出待定系数的值;
(2)由于A、D关于抛物线对称轴即y轴对称,那么连接BD,BD与y轴的交点即为所求的M点,可先求出直线BD的解析式,即可得到M点的坐标;
(3)设直线BC与y轴的交点为N,那么△ABM的面积即为梯形ABNO、△BMN、△AOM的面积差,由此可求出△ABM和△PAD的面积;在△PAD中,AD的长为定值,可根据其面积求出P点纵坐标的绝对值,然后代入抛物线的解析式中即可求出P点的坐标.
(2)由于A、D关于抛物线对称轴即y轴对称,那么连接BD,BD与y轴的交点即为所求的M点,可先求出直线BD的解析式,即可得到M点的坐标;
(3)设直线BC与y轴的交点为N,那么△ABM的面积即为梯形ABNO、△BMN、△AOM的面积差,由此可求出△ABM和△PAD的面积;在△PAD中,AD的长为定值,可根据其面积求出P点纵坐标的绝对值,然后代入抛物线的解析式中即可求出P点的坐标.
解答:解:(1)由题意可得:
,
解得
;
∴抛物线的解析式为:y=x2-4;
(2)由于A、D关于抛物线的对称轴(即y轴)对称,连接BD.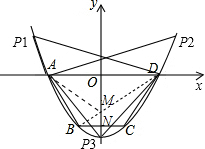
则BD与y轴的交点即为M点;
设直线BD的解析式为:y=kx+b(k≠0),则有:
,
解得
;
∴直线BD的解析式为y=x-2,点M(0,-2);
(3)设BC与y轴的交点为N,则有N(0,-3);
∴MN=1,BN=1,ON=3;
S△ABM=S梯形AONB-S△BMN-S△AOM=
(1+2)×3-
×2×2-
×1×1=2;
∴S△PAD=4S△ABM=8;
由于S△PAD=
AD•|yP|=8,
即|yP|=4;
当P点纵坐标为4时,x2-4=4,
解得x=±2
,
∴P1(-2
,4),P2(2
,4);
当P点纵坐标为-4时,x2-4=-4,
解得x=0,
∴P3(0,-4);
故存在符合条件的P点,且P点坐标为:P1(-2
,4),P2(2
,4),P3(0,-4).
|
解得
|
∴抛物线的解析式为:y=x2-4;
(2)由于A、D关于抛物线的对称轴(即y轴)对称,连接BD.

则BD与y轴的交点即为M点;
设直线BD的解析式为:y=kx+b(k≠0),则有:
|
解得
|
∴直线BD的解析式为y=x-2,点M(0,-2);
(3)设BC与y轴的交点为N,则有N(0,-3);
∴MN=1,BN=1,ON=3;
S△ABM=S梯形AONB-S△BMN-S△AOM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PAD=4S△ABM=8;
由于S△PAD=
| 1 |
| 2 |
即|yP|=4;
当P点纵坐标为4时,x2-4=4,
解得x=±2
| 2 |
∴P1(-2
| 2 |
| 2 |
当P点纵坐标为-4时,x2-4=-4,
解得x=0,
∴P3(0,-4);
故存在符合条件的P点,且P点坐标为:P1(-2
| 2 |
| 2 |
点评:此题主要考查了二次函数解析式的确定、函数图象交点及图形面积的求法,轴对称的性质等知识的综合应用能力;当所求图形不规则时,一般要将不规则图形转换为几个规则图形面积的和差来求.

练习册系列答案
相关题目
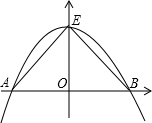 如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )
如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )| A、b=0 | B、S△ABE=c2 | C、ac=-1 | D、a+c=0 |
 (2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0). (2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).
(2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).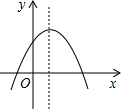 (1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( )
(1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( ) (1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;
(1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;