题目内容
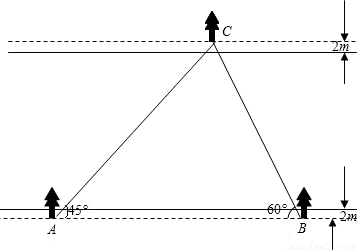
(2004•玉溪)如图,在某次植树活动中,初三(二)班的同学们沿河堤从A点到B点植树20棵,相邻两棵树之间的距离均为5米,完成任务后,数学兴趣小组的同学利用测角仪分别在A、B两点观测对岸C处的一棵小树,测得∠CAB和∠CBA分别为45°和60度.若小树距离河岸边都是2米,请你根据这些数据,帮助他们计算出河的宽度.(
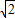 ≈1.414,
≈1.414,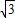 ≈1.732,结果保留整数)
≈1.732,结果保留整数)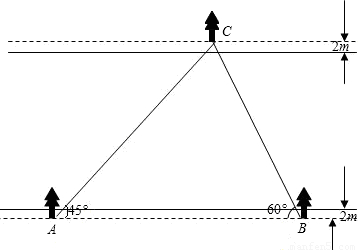
【答案】分析:算出△ABC的高,减去两个2即可.
解答: 解:做CD⊥AB于点D
解:做CD⊥AB于点D
∴∠ADC=∠BDC=90°
∵∠CAB=45°
设CD=x
∴AD=CD=x
同理可得到BD=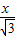
∵AD+BD=AB
∴x+ =(20-1)×5
=(20-1)×5
解得x≈60
∵小树距离河岸边都是2米
∴河岸宽是60-4=56米.
点评:解决本题的关键是利用所求线段表示出题中唯一给出的线段的长度.
解答:
 解:做CD⊥AB于点D
解:做CD⊥AB于点D∴∠ADC=∠BDC=90°
∵∠CAB=45°
设CD=x
∴AD=CD=x
同理可得到BD=
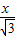
∵AD+BD=AB
∴x+
 =(20-1)×5
=(20-1)×5解得x≈60
∵小树距离河岸边都是2米
∴河岸宽是60-4=56米.
点评:解决本题的关键是利用所求线段表示出题中唯一给出的线段的长度.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
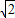 ≈1.414,
≈1.414,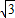 ≈1.732,结果保留整数)
≈1.732,结果保留整数)