题目内容
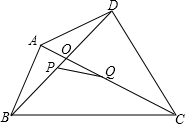 如图所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍.
如图所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍.
证明:设四边形ABCD对角线AC,BD中点分别是Q,P.
在△BDQ中,BQ2+DQ2=2PQ2+2•2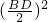 =2PQ2+
=2PQ2+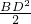
即2BQ2+2DQ2=4PQ2+BD2.①
在△ABC中,BQ是AC边上的中线,
所以BQ2= (2AB2+2BC2-AC2).②
(2AB2+2BC2-AC2).②
在△ACD中,QD是AC边上的中线,
所以DQ2= (2AD2+2DC2-AC2).③
(2AD2+2DC2-AC2).③
将②,③代入①得 (2AB2+2BC2-AC2)+
(2AB2+2BC2-AC2)+ (2AD2+2DC2-AC2)
(2AD2+2DC2-AC2)
=4PQ2+BD2,
即AB2+BC2+CD2+DA2=AC2+BD2+4PQ2.
分析:对角线中点连线为PQ,可看作△BDQ的中线,分别计算BQ2,DQ2,代入2BQ2+2DQ2=4PQ2+BD2.即可计算出即AB2+BC2+CD2+DA2=AC2+BD2+4PQ2.
点评:本题考查了直角三角形中勾股定理的运用,本题中分别求BQ2,DQ2,化简出2BQ2+2DQ2=4PQ2+BD2的等量关系式是解题的关键.
在△BDQ中,BQ2+DQ2=2PQ2+2•2
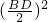 =2PQ2+
=2PQ2+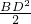
即2BQ2+2DQ2=4PQ2+BD2.①

在△ABC中,BQ是AC边上的中线,
所以BQ2=
 (2AB2+2BC2-AC2).②
(2AB2+2BC2-AC2).②在△ACD中,QD是AC边上的中线,
所以DQ2=
 (2AD2+2DC2-AC2).③
(2AD2+2DC2-AC2).③将②,③代入①得
 (2AB2+2BC2-AC2)+
(2AB2+2BC2-AC2)+ (2AD2+2DC2-AC2)
(2AD2+2DC2-AC2)=4PQ2+BD2,
即AB2+BC2+CD2+DA2=AC2+BD2+4PQ2.
分析:对角线中点连线为PQ,可看作△BDQ的中线,分别计算BQ2,DQ2,代入2BQ2+2DQ2=4PQ2+BD2.即可计算出即AB2+BC2+CD2+DA2=AC2+BD2+4PQ2.
点评:本题考查了直角三角形中勾股定理的运用,本题中分别求BQ2,DQ2,化简出2BQ2+2DQ2=4PQ2+BD2的等量关系式是解题的关键.

练习册系列答案
相关题目
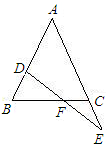 如图所示,在△ABC中,AB=AC,D是AB上任意一点,且BD=CE,连接DE交BC于F.
如图所示,在△ABC中,AB=AC,D是AB上任意一点,且BD=CE,连接DE交BC于F.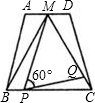 如图所示,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
如图所示,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形. 如图所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍.
如图所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍.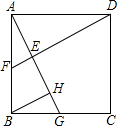 (2013•厦门)如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.
(2013•厦门)如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.