题目内容
【题目】已知直线y=﹣![]() x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣
x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣![]() (x﹣
(x﹣![]() )2+4上,能使△ABP为等腰三角形的点P的个数有( )
)2+4上,能使△ABP为等腰三角形的点P的个数有( )
A.3个 B.4个 C.5个 D.6个
【答案】A.
【解析】
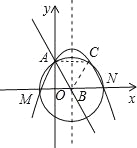
试题分析:以点B为圆心线段AB长为半径做圆,交抛物线于点C、M、N点,连接AC、BC,如图所示.
令一次函数y=﹣![]() x+3中x=0,则y=3,
x+3中x=0,则y=3,
∴点A的坐标为(0,3);
令一次函数y=﹣![]() x+3中y=0,则﹣
x+3中y=0,则﹣![]() x+3,
x+3,
解得:x=![]() ,
,
∴点B的坐标为(![]() ,0).
,0).
∴AB=2![]() .
.
∵抛物线的对称轴为x=![]() ,
,
∴点C的坐标为(2![]() ,3),
,3),
∴AC=2![]() =AB=BC,
=AB=BC,
∴△ABC为等边三角形.
令y=﹣![]() (x﹣
(x﹣![]() )2+4中y=0,则﹣
)2+4中y=0,则﹣![]() (x﹣
(x﹣![]() )2+4=0,
)2+4=0,
解得:x=﹣![]() ,或x=3
,或x=3![]() .
.
∴点E的坐标为(﹣![]() ,0),点F的坐标为(3
,0),点F的坐标为(3![]() ,0).
,0).
△ABP为等腰三角形分三种情况:
①当AB=BP时,以B点为圆心,AB长度为半径做圆,与抛物线交于C、M、N三点;
②当AB=AP时,以A点为圆心,AB长度为半径做圆,与抛物线交于C、M两点,;
③当AP=BP时,作线段AB的垂直平分线,交抛物线交于C、M两点;
∴能使△ABP为等腰三角形的点P的个数有3个.
故答案选A.

练习册系列答案
相关题目