题目内容
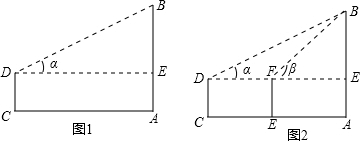
( 本题有A类、B类两题,A类每题8分,B类每题10分.你可以根据自己的学习情况,在两类题中只选做1题,如果两类题都做,则以A类题计分)(A类)如图1,在与旗杆AB相距20米的C处,用高1.20米的测角仪测得旗杆顶端B的仰角α=30°.求旗杆AB的高(精确到0.1米).
(B类)如图2,在C处用高1.20米的测角仪测得塔AB顶端B的仰角α=30°,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
我选做______类题,解答如下:

【答案】分析:A类:此题需要先解直角三角形△DBE,可得BE的数值;加上AE的大小,可得AB的数值.
B类:首先根据题意分析图形;本题涉及到两个直角三角形,解之求得GD与DF的大小,再利用DF=DG-FG=20,进而可解出BG的值,加上AG即可求出答案.
解答:解:(A类)在Rt△BED中,
BE=DEtan30°=ACtan30°.
AB=BE+EA=BE+CD≈12.7(米),
答:旗杆AB的高约为12.7米.
(B类)在Rt△BGF中,∵β=45°,∴BG=FG.
在Rt△BGD中,
BG=DGtan30°=(GF+FD)tan30°=(BG+20)tan30°.
∴BG=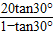
AB=AG+BG≈28.5(米)
答:塔AB的高约为28.5米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
B类:首先根据题意分析图形;本题涉及到两个直角三角形,解之求得GD与DF的大小,再利用DF=DG-FG=20,进而可解出BG的值,加上AG即可求出答案.
解答:解:(A类)在Rt△BED中,
BE=DEtan30°=ACtan30°.
AB=BE+EA=BE+CD≈12.7(米),
答:旗杆AB的高约为12.7米.
(B类)在Rt△BGF中,∵β=45°,∴BG=FG.
在Rt△BGD中,
BG=DGtan30°=(GF+FD)tan30°=(BG+20)tan30°.
∴BG=
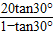
AB=AG+BG≈28.5(米)
答:塔AB的高约为28.5米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 ,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).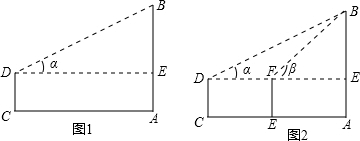 ,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).