题目内容
【题目】如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE. 求证:四边形ADCE是菱形.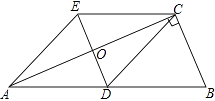
【答案】证明:∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形.
∴EC∥DB,且EC=DB.
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形ADCE是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形ADCE是菱形
【解析】欲证明四边形ADCE是菱形,需先证明四边形ADCE为平行四边形,然后再证明其对角线相互垂直即可.
【考点精析】关于本题考查的直角三角形斜边上的中线和菱形的判定方法,需要了解直角三角形斜边上的中线等于斜边的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能得出正确答案.

练习册系列答案
相关题目