题目内容
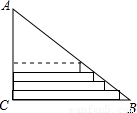
 红星中学高二(2)班在布置“五.四”青年节联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条.如图所示:在Rt△ACB中,AC=30cm,BC=40cm.依此裁下宽度为lcm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数
红星中学高二(2)班在布置“五.四”青年节联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条.如图所示:在Rt△ACB中,AC=30cm,BC=40cm.依此裁下宽度为lcm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数
- A.24
- B.25
- C.26
- D.27
C
分析:根据相似三角形对应边成比例,求出纸条长度是5cm时纸条的上边沿离顶点A的距离,然后再计算纸条的上边沿离BC的距离,便不难得到纸条的张数.
解答: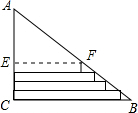 解:如图,设EF=5cm,
解:如图,设EF=5cm,
∵裁出的是矩形纸条,
∴EF∥BC,
∴△AEF∽△ACB,
∴ =
= ,即
,即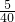 =
= ,解得AE=3.75cm,
,解得AE=3.75cm,
∴CE=AC-AE=30-3.75=26.25cm,
∵裁得的纸条的长都不小于5cm,
∴CE≤26.25cm,
∵纸条宽度为1cm,
∴CE最大是26cm,
∴最多可以裁得的纸条的张数为26.
故选C.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,根据题意得出相似三角形是解答此题的关键.
分析:根据相似三角形对应边成比例,求出纸条长度是5cm时纸条的上边沿离顶点A的距离,然后再计算纸条的上边沿离BC的距离,便不难得到纸条的张数.
解答:
 解:如图,设EF=5cm,
解:如图,设EF=5cm,∵裁出的是矩形纸条,
∴EF∥BC,
∴△AEF∽△ACB,
∴
 =
= ,即
,即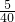 =
= ,解得AE=3.75cm,
,解得AE=3.75cm,∴CE=AC-AE=30-3.75=26.25cm,
∵裁得的纸条的长都不小于5cm,
∴CE≤26.25cm,
∵纸条宽度为1cm,
∴CE最大是26cm,
∴最多可以裁得的纸条的张数为26.
故选C.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,根据题意得出相似三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
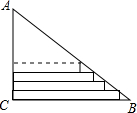 红星中学高二(2)班在布置“五.四”青年节联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条.如图所示:在Rt△ACB中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数( )
红星中学高二(2)班在布置“五.四”青年节联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条.如图所示:在Rt△ACB中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数( )