题目内容
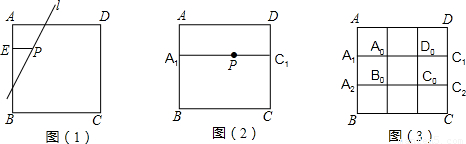
在一次课题学习中活动中,老师提出了如下一个问题:点P是正方形ABCD内的一点,过点P画直线l分别交正方形的两边于点M、N,使点P是线段MN的三等分点,这样的直线能够画几条?
经过思考,甲同学给出如下画法:
如图1,过点P画PE⊥AB于E,在EB上取点M,使EM=2EA,画直线MP交AD于N,则直线MN就是符合条件的直线l.
根据以上信息,解决下列问题:
(1)甲同学的画法是否正确?请说明理由;
(2)在图1中,能否画出符合题目条件的直线?如果能,请直接在图1中画出;
(3)如图2,A1,C1分别是正方形ABCD的边AB、CD上的三等分点,且A1C1∥AD.当点P在线段A1C1上时,能否画出符合题目条件的直线?如果能,可以画出几条?
(4)如图3,正方形ABCD边界上的A1,A2,B1,B2,C1,C2,D1,D2都是所在边的三等分点.当点P在正方形ABCD内的不同位置时,试讨论,符合题目条件的直线l的条数的情况.
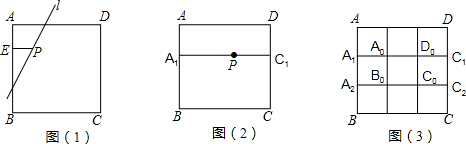
分析:(1)利用△MPE∽△MNA中的成比例线段可知EM=2EA,所以MP:MN=2:3,即点P是线段MN的一个三等分点;
(2)由(1)中的证明过程可知,在EB上取M1,使EM1=
AE,直线M1P就是满足条件的直线,所以能画出一条符合题目条件的直线;
(3)当点P在线段A1C1上,根据正方形的性质可知能够画出符合题目条件的直线有无数条;
(4)分情况讨论.
(2)由(1)中的证明过程可知,在EB上取M1,使EM1=
| 1 |
| 2 |
(3)当点P在线段A1C1上,根据正方形的性质可知能够画出符合题目条件的直线有无数条;
(4)分情况讨论.
解答:解:(1)甲同学的画法正确;
∵PE∥AD,
∴△MPE∽△MNA,
∴
=
,
∵EM=2EA,
∴MP:MN=2:3,
∴点P是线段MN的一个三等分点.
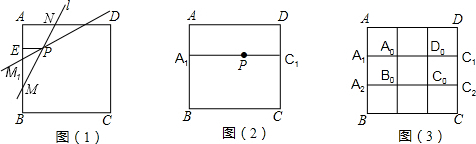
(2)能画出一个符合题目条件的直线,在EB上取M1,使EM1=
AE,直线M1P就是满足条件的直线,图2;
(3)若点P在线段A1C1上,能够画出符合题目条件的直线无数条,图3;
(4)若点P在A1C1,A2C2,B1D1,B2D2上时,可以画出无数条符合条件的直线l;
当点P在正方形A0B0C0D0内部时,不存在这样的直线l,使得点P是线段MN的三等分点;
当点P在矩形ABB1D1,CDD2B2,A0D0D2D1,B0B1B2C0内部时,过点P可画出两条符合条件的直线l,使得点P是线段MN的三等分点.
∵PE∥AD,
∴△MPE∽△MNA,
∴
| MP |
| MN |
| ME |
| MA |
∵EM=2EA,
∴MP:MN=2:3,
∴点P是线段MN的一个三等分点.

(2)能画出一个符合题目条件的直线,在EB上取M1,使EM1=
| 1 |
| 2 |
(3)若点P在线段A1C1上,能够画出符合题目条件的直线无数条,图3;
(4)若点P在A1C1,A2C2,B1D1,B2D2上时,可以画出无数条符合条件的直线l;
当点P在正方形A0B0C0D0内部时,不存在这样的直线l,使得点P是线段MN的三等分点;
当点P在矩形ABB1D1,CDD2B2,A0D0D2D1,B0B1B2C0内部时,过点P可画出两条符合条件的直线l,使得点P是线段MN的三等分点.
点评:主要考查了正方形的性质和复杂作图的运用.掌握正方形的性质并具备综合分析的能力是解题的关键.

练习册系列答案
相关题目