题目内容
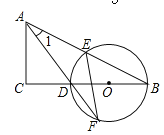
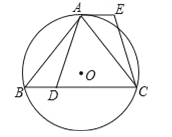
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据等弧所对的圆周角相等,得出∠B=∠ACB,再根据全等三角形的判定得△ABD≌△CAE,即可得出AD=CE;
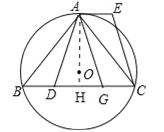
(2)连接AO并延长,交边BC于点H,由等腰三角形的性质和外心的性质得出AH⊥BC,再由垂径定理得BH=CH,得出CG与AE平行且相等.
试题解析:(1)在⊙O中,∵![]() ,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
(2)连接AO并延长,交边BC于点H,∵![]() ,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.
,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.

练习册系列答案
相关题目