题目内容
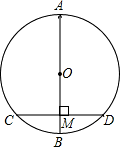 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于M,下列四个结论:
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于M,下列四个结论:
①CM=DM,②AC=AD,③ =
= ,④∠C=∠D.
,④∠C=∠D.
其中成立的有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:连接AC,AD,根据垂径定理判断求解.
解答: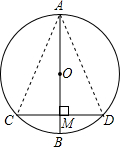 解:连接AC,AD,
解:连接AC,AD,
由垂径定理知,点M是CD的中点,点B是弧CD的中点,点A是弧CAD的中点,
则有:CM=DM,弧BC=弧BD,弧AC=弧AD,
由圆周角定理知,∠C=∠D,
∴①②④成立.③错误.
故选C.
点评:本题利用了:1、垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧.
2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
分析:连接AC,AD,根据垂径定理判断求解.
解答:
 解:连接AC,AD,
解:连接AC,AD,由垂径定理知,点M是CD的中点,点B是弧CD的中点,点A是弧CAD的中点,
则有:CM=DM,弧BC=弧BD,弧AC=弧AD,
由圆周角定理知,∠C=∠D,
∴①②④成立.③错误.
故选C.
点评:本题利用了:1、垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧.
2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
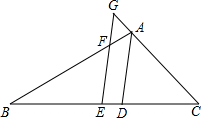 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.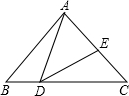 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.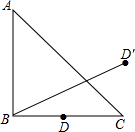 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=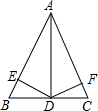 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有