题目内容
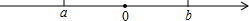已知有理数a，b在数轴上的位置如图所示，且|a|=|b|，则|a-b|+|a+b|可化简为（ ）分析：根据数轴可知a是负数，b是正数，然后判断出a-b与a+b的正负情况，并去掉绝对值号，合并同类项即可得解．
解答：解：根据数轴可得a＜0，b＞0，
∵|a|=|b|，
∴a-b＜0，a+b=0，
∴|a-b|+|a+b|=-a+b+a+b=2b．
故选D．
∵|a|=|b|，
∴a-b＜0，a+b=0，
∴|a-b|+|a+b|=-a+b+a+b=2b．
故选D．
点评：本题考查了绝对值与数轴，根据数轴判断出a、b的正负情况并去掉绝对值号是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
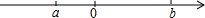已知有理数a、b在数轴上的位置如图所示，试用“＜”号按从小到大的顺序，将数a、b、0、-a、-b连接起来．
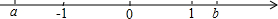已知有理数a，b在数轴上的对应点的位置如图，0表示原点．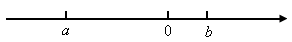
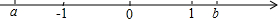已知有理数a，b在数轴上的对应点的位置如图，0表示原点．