题目内容
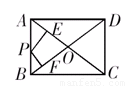
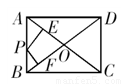
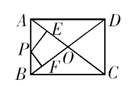
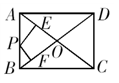
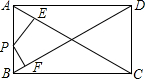如图，矩形ABCD两邻边分别为3，4，点P是矩形一边上任意一点，则点P到两条对角线AC、BD的距离之和PE+PF为分析：首先设未知线段为未知数，然后根据矩形的性质求出相似三角形，进而求解．
解答：解：设PE=x，PF=a，PB=y．
由∠PBF=∠ABD，∠PFB=∠DAB可得△ABD∽△FBP，
故
=
，
同理可证
=
，
故a+x=
×3=
．
故答案为：
．
由∠PBF=∠ABD，∠PFB=∠DAB可得△ABD∽△FBP，
故
| a |
| 4 |
| y |
| 5 |
同理可证
| x |
| 4 |
| 3-y |
| 5 |
故a+x=
| 4 |
| 5 |
| 12 |
| 5 |
故答案为：
| 12 |
| 5 |
点评：本题考查的是矩形的性质，要注意的是设线段的未知数，再进而证明相似三角形从而求解，难度中等．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
