题目内容
已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是分析:画出草图分析.因为周长是40,所以边长是10.根据对角线互相垂直平分得直角三角形,运用勾股定理求另一条对角线的长,最后根据菱形的面积等于对角线乘积的一半计算求解.
解答: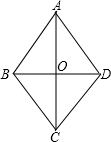 解:因为周长是40,所以边长是10.
解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S=
AC×BD=12×16×
=96.
故答案为96.
 解:因为周长是40,所以边长是10.
解:因为周长是40,所以边长是10.如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为96.
点评:本题考查了菱形的性质及其面积计算,主要利用菱形的对角线互相垂直平分及勾股定理来解决,要掌握菱形的面积有两种求法:(1)利用底乘以相应底上的高;(2)利用菱形的特殊性,菱形面积=12×两条对角线的乘积,具体用哪种方法要看已知条件来填空.

练习册系列答案
相关题目
已知菱形的周长为40,一条对角线为12,则这个菱形的面积为( )
| A、190 | B、96 | C、48 | D、40 |