题目内容
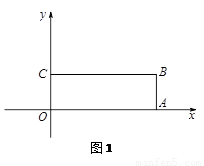
 已知如图,平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点C,点D的坐标分别为(0,4),(5,0),
已知如图,平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点C,点D的坐标分别为(0,4),(5,0),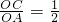 ,点P在BC边上运动(不与B,C重合),当△ODP是腰长为5的等腰三角形时,点P的坐标为:________.
,点P在BC边上运动(不与B,C重合),当△ODP是腰长为5的等腰三角形时,点P的坐标为:________.
(2,4)或(3,4)或(8,4)
分析:求出OA、BC,求出的P点的横坐标必须小于BC的长10,根据矩形的性质得出P的纵坐标是4(和C的纵坐标相等),分为两种情况:①当OP=OD=5时,在Rt△OCP中,由勾股定理求出CP即可;②当DP=OD=5时有P和P′两点,过D作DE⊥CB于E,由勾股定理求出PE,求出CP、CP′即可.
解答: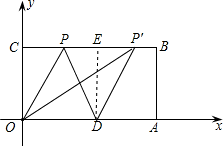 解:∵C(0,4)D(5,0),
解:∵C(0,4)D(5,0),
∴OC=4,OD=5,
∵四边形OABC是矩形,
∴BC∥OA,∠PCO=90°,
∵ =
= ,C(0,4),
,C(0,4),
∴OC=4,OA=10,
∵四边形OABC是矩形,
∴BC=OA=10,BC∥OA,
∴B(10,4),
分为两种情况:①当OP=OD=5时,在Rt△OCP中,由勾股定理得:CP=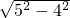 =3,
=3,
即P的坐标是(3,4);
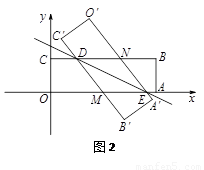
②以D为圆心,以5为半径作弧,交CB于P、P′,此时DP=DP′=5=OD,过D作DE⊥CB于E,
∵在Rt△EDP中,DE=OC=4,由勾股定理得:PE=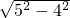 =3,
=3,
∴CP=5-3=2<BC,
∵P在BC上,BC∥OA,B(10,4),
∴P的坐标是(2,4);
当在P′处时,CP′=5+3=8<BC,
∵P′在BC上,BC∥OA,B(10,4),
此时P′的坐标是(8,4).
故答案为:(2,4)或(3,4)或(8,4).
点评:本题考查学生知识点是等腰三角形的性质、勾股定理、矩形的性质、坐标和图形变换等,注意:应进行分类讨论,题目比较好,难度适中.
分析:求出OA、BC,求出的P点的横坐标必须小于BC的长10,根据矩形的性质得出P的纵坐标是4(和C的纵坐标相等),分为两种情况:①当OP=OD=5时,在Rt△OCP中,由勾股定理求出CP即可;②当DP=OD=5时有P和P′两点,过D作DE⊥CB于E,由勾股定理求出PE,求出CP、CP′即可.
解答:
 解:∵C(0,4)D(5,0),
解:∵C(0,4)D(5,0),∴OC=4,OD=5,
∵四边形OABC是矩形,
∴BC∥OA,∠PCO=90°,
∵
 =
= ,C(0,4),
,C(0,4),∴OC=4,OA=10,
∵四边形OABC是矩形,
∴BC=OA=10,BC∥OA,
∴B(10,4),
分为两种情况:①当OP=OD=5时,在Rt△OCP中,由勾股定理得:CP=
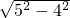 =3,
=3,即P的坐标是(3,4);
②以D为圆心,以5为半径作弧,交CB于P、P′,此时DP=DP′=5=OD,过D作DE⊥CB于E,
∵在Rt△EDP中,DE=OC=4,由勾股定理得:PE=
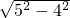 =3,
=3,∴CP=5-3=2<BC,
∵P在BC上,BC∥OA,B(10,4),
∴P的坐标是(2,4);
当在P′处时,CP′=5+3=8<BC,
∵P′在BC上,BC∥OA,B(10,4),
此时P′的坐标是(8,4).
故答案为:(2,4)或(3,4)或(8,4).
点评:本题考查学生知识点是等腰三角形的性质、勾股定理、矩形的性质、坐标和图形变换等,注意:应进行分类讨论,题目比较好,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
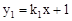 的图象与y轴交于点A,
的图象与y轴交于点A,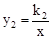 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐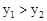 时x的取值范围。
时x的取值范围。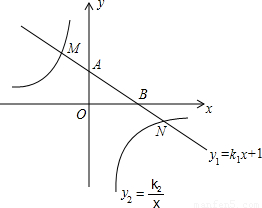
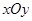 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐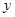 =-
=-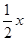 +
+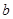 交折线O-A-B于点E.
交折线O-A-B于点E.