题目内容
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).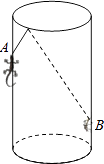
【答案】1.3
【解析】解:如图:

∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2﹣0.3+AE=1.2m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B= ![]()
= ![]()
=1.3(m).
所以答案是:1.3.
【考点精析】利用勾股定理的概念和圆柱的相关计算对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;圆柱的体积: V圆柱=πR2h.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目