Question

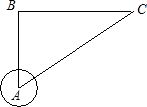如图，一艘渔政船从小岛A处出发，向正北方向以每小时20海里的速度行驶了1.5小时到达B处执行任务，再向正东方向以相同的速度行驶了2小时到达C处继续执行任务，然后以相同的速度直接从C处返回A处．
（1）分别求AB、BC的长；
（2）问返回时比出去时节省了多少时间？

Answer 1

分析：（1）根据小岛A处出发，以每小时20海里的速度和行驶的时间即可分别求出AB，BC的长；
（2）根据勾股定理求出AC的长，然后根据“相同的速度”这一条件求出返回所用时间，再用总时间减去即可．

解答：解：（1）AB=20×1.5=30（海里），BC=20×2=40（海里）；

（2）在△ABC中，∠ABC=90，
由勾股定理得，AC=

AB2+BC2

=

302+402

=50（海里）；
返回时所用时间为：

50

20

=2.5小时，
出去时所用时间为：2+1.5=3.5小时，
则返回时比出去时节省的时间为：3.5-2.5=1小时．
答：（1）AB的长为：30海里；BC的长为：50海里；
（2）问返回时比出去时节省了1小时．

点评：此题主要考查学生对勾股定理的应用这一知识点理解和掌握，比较简单，属于基础题．