题目内容
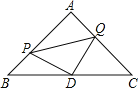
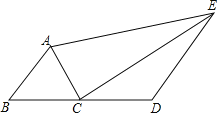
【题目】如图,在四边形ABDE中,C是BD边的中点.若AC平分∠BAE,∠ACE=90°,猜想线段AE、AB、DE的长度满足的数量关系为并证明.
【答案】AE=AB+DE.
【解析】
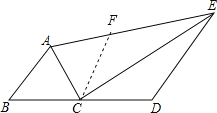
试题分析:在AE上取一点F,使AF=AB,即可得出△ACB≌△ACF,就可以得出BC=FC,∠ACB=∠ACF,就可以得出△CEF≌△CED.就可以得出结论.
解:AE=AB+DE;
理由:在AE上取一点F,使AF=AB.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
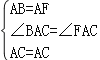 ,
,
∴△ACB≌△ACF(SAS),
∴BC=FC,∠ACB=∠ACF.
∵C是BD边的中点.
∴BC=CD,
∴CF=CD.
∵∠ACE=90°,
∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°
∴∠ECF=∠ECD.
在△CEF和△CED中,
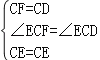 ,
,
∴△CEF≌△CED(SAS),
∴EF=ED.
∵AE=AF+EF,
∴AE=AB+DE.

练习册系列答案
相关题目