题目内容
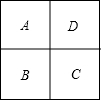
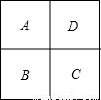
如图，一个田字形的区域A、B、C、D栽种观赏植物，要求同一个区域中种同一种植物，相邻的两块种不同的植物，现有4种不同的植物可供选择，那么有
84
84
种栽种方案．分析：本题可以根据A，C所种的种数相同和不同来分类，然后再考虑B，D有多少种种法，最后求得结果．
解答：解：若A，C种同一种植物，则A，C有4×1种栽种方法，B，D都有3种栽种法，共有4×3×3=36种栽种方案；
若A，C种不同的植物，则有4×3种栽种法，B，D都有2种栽种法，一共有4×3×2×2=48种栽种法．
所以共有36+48=84种．
故答案为：84．
若A，C种不同的植物，则有4×3种栽种法，B，D都有2种栽种法，一共有4×3×2×2=48种栽种法．
所以共有36+48=84种．
故答案为：84．
点评：本题考查理解题意能力，关键是分类思想的运用以及意全面地考虑问题，否则容易得到错误的结果．
练习册系列答案
全能练考卷系列答案
相关题目
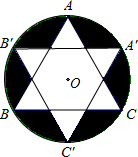如图是一个跳棋棋盘的示意图，它可以看成将等边△ABC绕着中心O旋转60°，再以点O为圆心，OA长为半径作圆得到．若AB=3，则棋子摆放区域（阴影部分）的面积为（ ）A、3π-4
| ||
B、3π-3
| ||
C、3π-2
| ||
D、3π-
|
