题目内容
如图，有一拱桥呈抛物线型，已知水位在AB位置时，水面宽AB=20米，水位上升5米就达到警戒水位线CD，这时水面宽CD=10
米。若洪水到来时，以每小时0.2米的速度上升，求水过警戒线后几小时淹到拱桥顶？
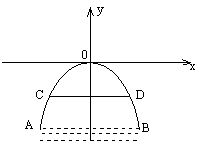
设抛物线解析式为y=ax2(a<0)
点B坐标为(10，y)，则点D坐标为(
，解得
∴y= -
当x=5时，y= -5
∴
(小时)
练习册系列答案
津桥教育计算小状元系列答案
相关题目
津桥教育计算小状元系列答案题目内容
如图，有一拱桥呈抛物线型，已知水位在AB位置时，水面宽AB=20米，水位上升5米就达到警戒水位线CD，这时水面宽CD=10米。若洪水到来时，以每小时0.2米的速度上升，求水过警戒线后几小时淹到拱桥顶？
设抛物线解析式为y=ax2(a<0)
点B坐标为(10，y)，则点D坐标为(
，解得
∴y= -
当x=5时，y= -5
∴(小时)
津桥教育计算小状元系列答案
如图，有一拱桥呈抛物线型，已知水位在AB位置时，水面宽AB=20米，水位上升5米就达到警戒水位线CD，这时水面宽CD=10