题目内容
 (2013•湖州一模)如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为
(2013•湖州一模)如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为| 18 |
| 5 |
| 18 |
| 5 |
分析:在Rt△ABC中,由勾股定理可直接求得AB的长;过C作CM⊥AB,交AB于点M,由垂径定理可得M为AE的中点,在Rt△ACM中,根据勾股定理得AM的长,从而得到AE的长.
解答:解:在Rt△ABC中,AC=3,BC=4;
根据勾股定理,得AB=5.
过C作CM⊥AB,交AB于点M,如图所示,

由垂径定理可得M为AE的中点,
∵S△ABC=
AC•BC=
AB•CM,且AC=3,BC=4,AB=5,
∴CM=
,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(
)2,
解得:AM=
,
∴AE=2AM=
.
故答案为:
.
根据勾股定理,得AB=5.
过C作CM⊥AB,交AB于点M,如图所示,

由垂径定理可得M为AE的中点,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=
| 12 |
| 5 |
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(
| 12 |
| 5 |
解得:AM=
| 9 |
| 5 |
∴AE=2AM=
| 18 |
| 5 |
故答案为:
| 18 |
| 5 |
点评:此题主要考查学生对勾股定理及垂径定理的理解及运用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (2013•湖州一模)如图,一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,它的母线长是5米,底面半径为3米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)
(2013•湖州一模)如图,一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,它的母线长是5米,底面半径为3米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)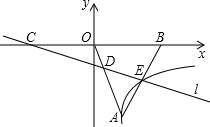 (2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )
(2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )