题目内容
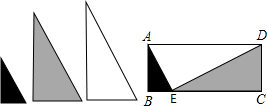如图，用形状相同、大小不等的3块直角三角形木板，恰好能拼成如图所示的四边形ABCD，如果AE=2，CE=3BE=3，那么这个四边形的面积是分析：在直角△ABE，中根据AE，BE可以计算AB的长度，且BE=CE+BE，根据BC、AB即可计算矩形ABCD的面积．
解答：解：在直角△ABE中，BE=1，AE=2，且AB为直角边
则AB=
=
，
且BC=BE+CE=1+3=4，
∴矩形ABCD的面积为S=BC•AB=4
．
故答案为：4
．
则AB=
| AE2-BE2 |
| 3 |
且BC=BE+CE=1+3=4，
∴矩形ABCD的面积为S=BC•AB=4
| 3 |
故答案为：4
| 3 |
点评：本题考查了勾股定理在实际生活中的运用，考查了勾股定理的灵活运用，本题中正确的计算AB的长度是解题的关键．
练习册系列答案
相关题目
三等分，分点为
，过
作
的平行线，交
于点
，得多边形
，请用四个这样的小多边形，拼成一个形状相同的大多边形．
