题目内容
如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡 度i=1:
度i=1:| 3 |
(1)求小山的高度;
(2)求铁架的高度.(
| 3 |
分析:(1)过D作DF垂直于坡底的水平线BC于点F,再由斜坡的坡比的概念,可得坡角为30°;解Rt△DFB可得DF即山高;
(2)首先根据题意分析图形;本题涉及到两个直角三角形Rt△AED与Rt△ACB,解可得AC与BC的大小,再由AC=AE+EC,进而可求出答案.
(2)首先根据题意分析图形;本题涉及到两个直角三角形Rt△AED与Rt△ACB,解可得AC与BC的大小,再由AC=AE+EC,进而可求出答案.
解答: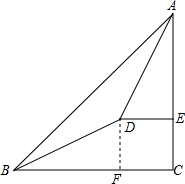 解:(1)如图,过D作DF垂直于坡底的水平线BC于点F.
解:(1)如图,过D作DF垂直于坡底的水平线BC于点F.
由已知,斜坡的坡比i=1:
,于是tan∠DBC=
,
∴坡角∠DBC=30°.
于是在Rt△DFB中,DF=DBsin30°=25,
即小山高为25米.
(2)设铁架的高AE=x.
在Rt△AED中,已知∠ADE=60°,于是DE=
=
x,
在Rt△ACB中,已知∠ABC=45°,
∵AC=AE+EC=AE+DF=x+25,
又BC=BF+FC=BF+DE=25
+
x,
由AC=BC,得x+25=25
+
x.
∴x=25
≈43.3,即铁架高43.3米.
 解:(1)如图,过D作DF垂直于坡底的水平线BC于点F.
解:(1)如图,过D作DF垂直于坡底的水平线BC于点F.由已知,斜坡的坡比i=1:
| 3 |
| ||
| 3 |
∴坡角∠DBC=30°.
于是在Rt△DFB中,DF=DBsin30°=25,
即小山高为25米.
(2)设铁架的高AE=x.
在Rt△AED中,已知∠ADE=60°,于是DE=
| AE |
| tan60° |
| ||
| 3 |
在Rt△ACB中,已知∠ABC=45°,
∵AC=AE+EC=AE+DF=x+25,
又BC=BF+FC=BF+DE=25
| 3 |
| ||
| 3 |
由AC=BC,得x+25=25
| 3 |
| ||
| 3 |
∴x=25
| 3 |
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 如图,小山的顶部是一块平地DE,在这块平地上有一高压输电的铁架AE,小山的斜坡BD的坡度i=1:
如图,小山的顶部是一块平地DE,在这块平地上有一高压输电的铁架AE,小山的斜坡BD的坡度i=1: ,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。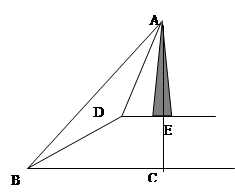
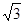 ,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
 如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度
如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度