题目内容
甲乙二人同时登山,甲登上A处停下来,拍照游玩,后与乙同时登上山顶.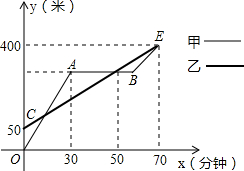 两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答以下问题:
两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答以下问题:
(1)乙登山的速度是
(2)甲在A处游玩后,以与先前相同的速度继续爬山,结果与乙同时到达山顶,甲爬后一段山路BE用了多少分钟?
(3)求BE段甲的y与x的函数关系式.
 两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答以下问题:
两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答以下问题:(1)乙登山的速度是
5
5
米/分,A处的高度是300
300
米.(2)甲在A处游玩后,以与先前相同的速度继续爬山,结果与乙同时到达山顶,甲爬后一段山路BE用了多少分钟?
(3)求BE段甲的y与x的函数关系式.
分析:(1)从图象可以看出,乙登山的路程是400-50=350(米),用的时间是70分钟,根据速度公式即可求出乙登山的速度;求出当乙登山的时间是50分钟时,路程是250米,即可得出A处的高度;
(2)求出BE对应的路程和甲登山的速度,即可求出甲爬后一段山路BE用的时间;
(3)设BE段甲的y与x的函数关系式是y=kx+b,把(60.300)和(70.400)代入求出即可.
(2)求出BE对应的路程和甲登山的速度,即可求出甲爬后一段山路BE用的时间;
(3)设BE段甲的y与x的函数关系式是y=kx+b,把(60.300)和(70.400)代入求出即可.
解答:解:(1)∵从图象可以看出,乙登山的路程是400-50=350(米),用的时间是70分钟,
∴乙登山的速度是350÷70=5(米/分);
当乙登山的时间是50分钟时,路程是50分×5米/分=250米,
即A处的高度是250米+50米=300米.
故答案为:5,300;
(2)∵BE对应的路程是400米-300米=100米,
甲登山的速度是300米÷30分=10米/分,
∴甲爬后一段山路BE用了100÷10=10(分钟),
答:甲爬后一段山路BE用了10分钟;
(3)∵设BE段甲的y与x的函数关系式是y=kx+b,
70分钟-10分钟=60分钟,
∴把(60.300)和(70.400)代入得:
,
解得:k=10,b=-300,
即BE段甲的y与x的函数关系式是y=10x-300.
∴乙登山的速度是350÷70=5(米/分);
当乙登山的时间是50分钟时,路程是50分×5米/分=250米,
即A处的高度是250米+50米=300米.
故答案为:5,300;
(2)∵BE对应的路程是400米-300米=100米,
甲登山的速度是300米÷30分=10米/分,
∴甲爬后一段山路BE用了100÷10=10(分钟),
答:甲爬后一段山路BE用了10分钟;
(3)∵设BE段甲的y与x的函数关系式是y=kx+b,
70分钟-10分钟=60分钟,
∴把(60.300)和(70.400)代入得:
|
解得:k=10,b=-300,
即BE段甲的y与x的函数关系式是y=10x-300.
点评:本题考查了一次函数的应用,主要考查学生能否把实际问题转化成数学问题,题目比较好,有一定的难度,考查了学生的观察能力,用了数形结合思想和转化思想.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
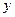 (米)与登山时间
(米)与登山时间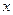 (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: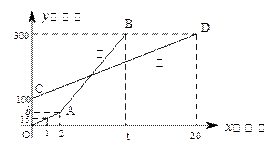
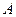 地提速时距地面的高度
地提速时距地面的高度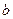 为 ____米;
为 ____米; (米)与登山时间
(米)与登山时间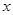 (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: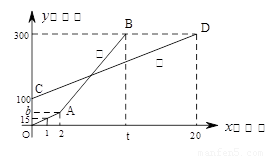
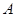 地提速时距地面的高度
地提速时距地面的高度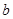 为 ____米;
为 ____米; (米)与登山时间
(米)与登山时间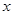 (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: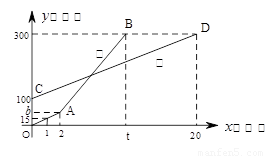
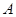 地提速时距地面的高度
地提速时距地面的高度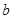 为 ____米;
为 ____米;