题目内容
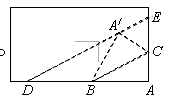
(如图所示)取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图(1);第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为![]() ,得Rt△
,得Rt△![]() ,如图(2);第三步:沿
,如图(2);第三步:沿![]() 线折叠得折痕EF,如图(3).利用展开图(4)探究:
线折叠得折痕EF,如图(3).利用展开图(4)探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.

答案:
解析:
解析:
|
(1)△AEF是等边三角形. 理由:由折纸过程知△BAE≌ 所以△EAF为等边三角形. (2)不一定;略. |

练习册系列答案
相关题目
 10、如图所示,一张矩形纸片,要折叠出一个最大的正方形,小明把矩形上的一个角沿折痕AE翻折上去,使AB与AD边上的AF重合,则四边形ABEF就是一个大的正方形,他判定的方法是
10、如图所示,一张矩形纸片,要折叠出一个最大的正方形,小明把矩形上的一个角沿折痕AE翻折上去,使AB与AD边上的AF重合,则四边形ABEF就是一个大的正方形,他判定的方法是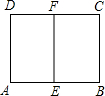 如图所示,一张矩形纸片ABCD的长AB=acm,宽BC=bcm,E、F分别为AB、CD的中点,这张纸片沿直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )
如图所示,一张矩形纸片ABCD的长AB=acm,宽BC=bcm,E、F分别为AB、CD的中点,这张纸片沿直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )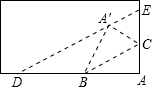 如图所示,一张矩形纸片沿BC折叠,顶点A落在点A′处,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是
如图所示,一张矩形纸片沿BC折叠,顶点A落在点A′处,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是