题目内容
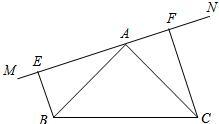 24、如图,已知:在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A点的直线MN作垂线,垂足为E、F.求证:AE=CF.
24、如图,已知:在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A点的直线MN作垂线,垂足为E、F.求证:AE=CF.分析:BE、CF为直线MN的垂线,∠BEA=∠AFC=90°,又∠BAC=90°,利用互余关系可证∠FCA=∠EAB,已知AB=AC,可证△FAC≌△EBA,故AE=CF.
解答:证明:∵BE⊥MN,CF⊥MN,
∴∠AEB=∠CFA=90°.
∴∠FAC+∠FCA=90°.
∵∠BAC=90°,
∴∠FAC+∠EAB=90°.
∴∠FCA=∠EAB.
∵AB=AC,
∴△FAC≌△EBA.
∴AE=CF.
∴∠AEB=∠CFA=90°.
∴∠FAC+∠FCA=90°.
∵∠BAC=90°,
∴∠FAC+∠EAB=90°.
∴∠FCA=∠EAB.
∵AB=AC,
∴△FAC≌△EBA.
∴AE=CF.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
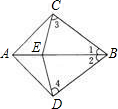
 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.

