题目内容
(2013•宝应县一模)抛物线y=-x2+bx+c与x轴交与A(1,0),B(-3,0)两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
分析:(1)将点A、点B的坐标代入可求出b、c的值,继而可得出该抛物线的解析式;
(2)连接BC,则BC与对称轴的交点,即是点Q的位置,求出直线BC的解析式后,可得出点Q的坐标.
(2)连接BC,则BC与对称轴的交点,即是点Q的位置,求出直线BC的解析式后,可得出点Q的坐标.
解答:解(1)把A(1,0)、B(-3,0)代入抛物线解析式可得:
,
解得:
故抛物线的解析式为y=-x2-2x+3.
(2)存在.
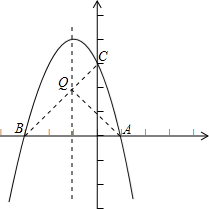
由题意得,点B与点A关于抛物线的对称轴对称,连接BC,则BC与抛物线对称轴的交点是点Q的位置,
设直线BC解析式为y=kx+b,把B(-3,0)、C(0,3)代入得:
,
解得:
,
则直线BC的解析式为y=x+3,
令QX=-1 得Qy=2,
故点Q的坐标为:(-1,2).
|
解得:
|
故抛物线的解析式为y=-x2-2x+3.
(2)存在.

由题意得,点B与点A关于抛物线的对称轴对称,连接BC,则BC与抛物线对称轴的交点是点Q的位置,
设直线BC解析式为y=kx+b,把B(-3,0)、C(0,3)代入得:
|
解得:
|
则直线BC的解析式为y=x+3,
令QX=-1 得Qy=2,
故点Q的坐标为:(-1,2).
点评:本题考查了二次函数的综合运用,涉及了顶点坐标的求解、三角形的面积及轴对称求最短路径的知识,解答本题的关键是熟练各个知识点,注意培养自己解综合题的能力.

练习册系列答案
相关题目
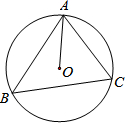 (2013•宝应县一模)如图,⊙O为锐角△ABC的外接圆,已知∠BAO=18°,那么∠C的度数为
(2013•宝应县一模)如图,⊙O为锐角△ABC的外接圆,已知∠BAO=18°,那么∠C的度数为 (2013•宝应县一模)如图,将△APB绕点B按逆时针方向旋转90°后得到△A1P1B.若BP=2,则线段PP1的长为
(2013•宝应县一模)如图,将△APB绕点B按逆时针方向旋转90°后得到△A1P1B.若BP=2,则线段PP1的长为