题目内容
晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米．又知自己身高1.80米，两盏路灯的高相同，两盏路灯之间的距离为12米．则路灯的高为分析：利用相似三角形的相似比，列出方程，通过解方程求出路灯的高即可．
解答：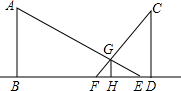
解：设路灯的高为x米，
∵GH⊥BD，AB⊥BD，
∴GH∥AB．
∴△EGH∽△EAB．
∴
=
①．
同理△FGH∽△FCD
=
②．
∴
=
=
．
∴
=
．
解得EB=11米，代入①得
=
，
解得x=6.6．
故答案为：6.6．
解：设路灯的高为x米，∵GH⊥BD，AB⊥BD，
∴GH∥AB．
∴△EGH∽△EAB．
∴
| GH |
| x |
| EH |
| EB |
同理△FGH∽△FCD
| GH |
| x |
| FH |
| FD |
∴
| EH |
| EB |
| FH |
| FD |
| EH+FH |
| EB+FD |
∴
| 3 |
| EB |
| 4.5 |
| 12+4.5 |
解得EB=11米，代入①得
| 1.8 |
| x |
| 3 |
| 11 |
解得x=6.6．
故答案为：6.6．
点评：本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求出路灯的高，体现了转化的思想．
练习册系列答案
相关题目
晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米．又知自己身高1.80米，两盏路灯的高相同，两盏路灯之间的距离为12米，则路灯的高为
晚上，小亮走在大街上时发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3m，左边的影子长为1.5m，又知自己身高1.80m，两盏路灯的高相同，两盏路灯之间的距离为12m，则路灯的高为（ ）
