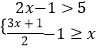题目内容
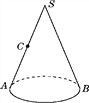
【题目】已知:如图,观察图形回答下面的问题:
(1)此图形的名称为________.
(2)请你与同伴一起做一个这样的物体,并把它沿AS剪开,铺在桌面上,则它的侧面展开图是一个________.
(3)如果点C是SA的中点,在A处有一只蜗牛,在C处恰好有蜗牛想吃的食品,但它又不能直接沿AC爬到C处,只能沿此立体图形的表面爬行,你能在侧面展开图中画出蜗牛爬行的最短路线吗?
(4)SA的长为10,侧面展开图的圆心角为90°,请你求出蜗牛爬行的最短路程.
【答案】 (1)圆锥 (2)扇形(3)见解析(4)![]()
【解析】试题分析:(1)根据几何体的特点可判断此图图形为圆锥,(2)圆锥的侧面展开图是扇形,(3)要求蜗牛爬行的最短距离,需将圆锥的侧面展开,进而根据”两点之间线段最短”得出结果,(4)已知圆锥侧面展开图的夹角为90°,则可得到最短路径是直角三角形的斜边,根据已知确定两直角边的长,即可利用勾股定理求解.
解:(1)圆锥 (2)扇形
(3)把此立体图形的侧面展开,如图所示,AC为蜗牛爬行的最短路线.
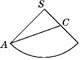
(4)在Rt△ASC中,由勾股定理,得AC2=102+52=125,
∴AC=![]() =
=![]() .
.
故蜗牛爬行的最短路程为![]() .
.

练习册系列答案
相关题目