题目内容
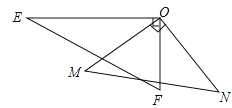
【题目】如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是 . 
【答案】![]()
【解析】解:如图,连接OM交AB于点C,连接OA、OB,
由题意知,OM⊥AB,且OC=MC= ![]() ,在RT△AOC中,∵OA=1,OC=
,在RT△AOC中,∵OA=1,OC= ![]() ,∴cos∠AOC=
,∴cos∠AOC= ![]() =
= ![]() ,AC=
,AC= ![]() =
= ![]() ∴∠AOC=60°,AB=2AC=
∴∠AOC=60°,AB=2AC= ![]() ,
,
∴∠AOB=2∠AOC=120°,
则S弓形ABM=S扇形OAB﹣S△AOB
= ![]() ﹣
﹣ ![]() ×
× ![]() ×
× ![]() =
= ![]() ﹣
﹣ ![]() ,
,
S阴影=S半圆﹣2S弓形ABM
= ![]() π×12﹣2(
π×12﹣2( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() .
.
故答案为: ![]() ﹣
﹣ ![]() .
.
连接OM交AB于点C,连接OA、OB,根据题意OM⊥AB且OC=MC= ![]() ,继而求出∠AOC=60°、AB=2AC=
,继而求出∠AOC=60°、AB=2AC= ![]() ,然后根据S弓形ABM=S扇形OAB﹣S△AOB、S阴影=S半圆﹣2S弓形ABM计算可得答案.本题考查了轴对称的性质的运用、勾股定理的运用、三角函数值的运用、扇形的面积公式的运用、三角形的面积公式的运用,解答时运用轴对称的性质求解是关键.
,然后根据S弓形ABM=S扇形OAB﹣S△AOB、S阴影=S半圆﹣2S弓形ABM计算可得答案.本题考查了轴对称的性质的运用、勾股定理的运用、三角函数值的运用、扇形的面积公式的运用、三角形的面积公式的运用,解答时运用轴对称的性质求解是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目