题目内容
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
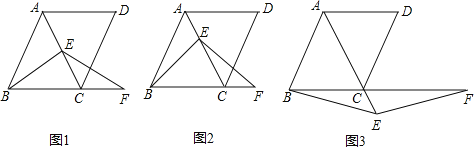
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
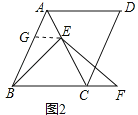
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
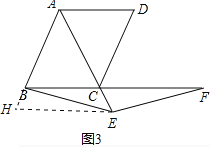
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)△ABC的面积=![]() ;(2)见解析;(3)成立,证明见解析.
;(2)见解析;(3)成立,证明见解析.
【解析】
试题分析:(1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;
(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作EH∥BC交AB的延长线于H,证明△BHE≌△ECF,得到BE=EF.
解:(1)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,又E是线段AC的中点,
∴BE⊥AC,AE=![]() AB=1,
AB=1,
∴BE=![]() ,
,
∴△ABC的面积=![]() ×AC×BE=
×AC×BE=![]() ;
;
(2)如图2,作EG∥BC交AB于G,
∵△ABC是等边三角形,
∴△AGE是等边三角形,
∴BG=CE,
∵EG∥BC,∠ABC=60°,
∴∠BGE=120°,
∵∠ACB=60°,
∴∠ECF=120°,
∴∠BGE=∠ECF,
在△BGE和△ECF中,
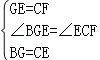 ,
,
∴△BGE≌△ECF,
∴EB=EF;
(3)成立,
如图3,作EH∥BC交AB的延长线于H,
∵△ABC是等边三角形,
∴△AHE是等边三角形,
∴BH=CE,
在△BHE和△ECF中,
 ,
,
∴△BHE≌△ECF,
∴EB=EF.

练习册系列答案
相关题目