题目内容
 如图,在反比例函数y=
如图,在反比例函数y=| 4 | x |
3
3
.分析:先根据题意求出点P1、P2、P3、P4的坐标,再把所有的阴影部分向左平移,则所有阴影部分的面积恰好等于矩形P1ABC的面积,再利用矩形的面积公式解答即可.
解答: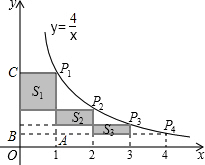 解:∵在反比例函数y=
解:∵在反比例函数y=
(x>0)的图象上,点P1、P2、P3、P4,它们的横坐标依次是1、2、3、4,
∴P1(1,4),P2(2,2)P3(3,
),P4(4,1),
∴P1A=4-1=3,
由图可知,所有的阴影部分向左平移,则所有阴影部分的面积恰好等于矩形P1ABC的面积,
∴S矩形P1ABC=1×3=3.
∴S1+S2+S3=3.
故答案为:3.
 解:∵在反比例函数y=
解:∵在反比例函数y=| 4 |
| x |
∴P1(1,4),P2(2,2)P3(3,
| 4 |
| 3 |
∴P1A=4-1=3,
由图可知,所有的阴影部分向左平移,则所有阴影部分的面积恰好等于矩形P1ABC的面积,
∴S矩形P1ABC=1×3=3.
∴S1+S2+S3=3.
故答案为:3.
点评:本题考查的是反比例函数系数k的几何意义,根据题意得出所有阴影部分的面积恰好等于矩形P1ABC的面积是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在反比例函数
如图,在反比例函数 ,S2,…,Sn,则Sn=
,S2,…,Sn,则Sn=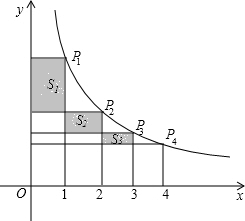 如图,在反比例函数y=
如图,在反比例函数y= n,求:
n,求: (2012•瑞安市模拟)如图,在反比例函数
(2012•瑞安市模拟)如图,在反比例函数