题目内容
为防水患,在漓江上游修筑了防洪堤,其横截面为一梯形(如图所示),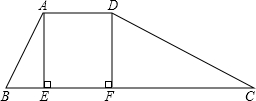 堤的上底宽AD和堤高DF都是6米,其中∠B=∠CDF.
堤的上底宽AD和堤高DF都是6米,其中∠B=∠CDF.(1)求证:△ABE∽△CDF;
(2)如果tanB=2,求堤的下底BC的长.
分析:(1)要证两三角形相似,要找齐两组对应角相等,这两个三角形中,已知了∠B=∠CDF,∠AEB和∠CFD是一组直角,因此就构成了判定相似三角形的条件.
(2)求BC的关键是求BE、CF的长,已知了∠B的正切值,由(1)的相似三角形可得出∠B=∠FDC,那么∠FDC的正切值也就得出了.可在直角三角形ABE和CDF中,用DF的长和∠B、∠CDF的正切函数求出BE、CF,也就能求出BC的长.
(2)求BC的关键是求BE、CF的长,已知了∠B的正切值,由(1)的相似三角形可得出∠B=∠FDC,那么∠FDC的正切值也就得出了.可在直角三角形ABE和CDF中,用DF的长和∠B、∠CDF的正切函数求出BE、CF,也就能求出BC的长.
解答:(1)证明:∠B=∠CDF,∠AEB=∠CFD
∴△ABE∽△CDF;
(2)解:在Rt△ABE中,tanB=
=2,AE=6
∴BE=
AE=
DF=3
在Rt△DFC中,∠CDF=∠B,DF=6∴tan∠CDF=
=2
∴FC=12
即BC=BE+EF+FC=3+6+12=21(m).
∴△ABE∽△CDF;
(2)解:在Rt△ABE中,tanB=
| AE |
| BE |
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△DFC中,∠CDF=∠B,DF=6∴tan∠CDF=
| FC |
| DF |
∴FC=12
即BC=BE+EF+FC=3+6+12=21(m).
点评:本题主要考查了相似三角形的判定以及解直角三角形的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
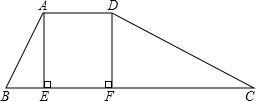 堤的上底宽AD和堤高DF都是6米,其中∠B=∠CDF.
堤的上底宽AD和堤高DF都是6米,其中∠B=∠CDF.

