题目内容
若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是
称为x的差倒数,如2的差倒数是 ;-1的差倒数为
;-1的差倒数为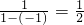 ,现已知x
,现已知x ,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2013=________.
,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2013=________.
4
分析:根据差倒数的定义分别计算出x1=- ,x2=
,x2= ;x3=4,x4=-
;x3=4,x4=- ,则得到从x1开始每3个值就循环,而2013=3×671,所以x2013=x3=4.
,则得到从x1开始每3个值就循环,而2013=3×671,所以x2013=x3=4.
解答:∵x1=- ,
,
∴x2= =
= ;
;
x3= =4;
=4;
x4= =-
=- ;
;
∴x5= ,
,
…,
∵2013=3×671,
∴x2013=x3=4.
故答案为4.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
分析:根据差倒数的定义分别计算出x1=-
 ,x2=
,x2= ;x3=4,x4=-
;x3=4,x4=- ,则得到从x1开始每3个值就循环,而2013=3×671,所以x2013=x3=4.
,则得到从x1开始每3个值就循环,而2013=3×671,所以x2013=x3=4.解答:∵x1=-
 ,
,∴x2=
 =
= ;
;x3=
 =4;
=4;x4=
 =-
=- ;
;∴x5=
 ,
,…,
∵2013=3×671,
∴x2013=x3=4.
故答案为4.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 称为x的差倒数,如2的差倒数是
称为x的差倒数,如2的差倒数是 ,-1的差倒数为
,-1的差倒数为 ,现已知
,现已知 ,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2012= .
,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2012= . 称为x的差倒数,如2的差倒数是
称为x的差倒数,如2的差倒数是 ,-1的差倒数为
,-1的差倒数为 ,现已知
,现已知 ,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2012= .
,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2012= .