��Ŀ����
����Ŀ����ͼ1����ֱ������ϵxoy�У�O������ԭ�㣬��A��x�������ϣ�OA=12 ![]() cm����B��y����������ϣ�OB=12cm������P�ӵ�O��ʼ��OA��2
cm����B��y����������ϣ�OB=12cm������P�ӵ�O��ʼ��OA��2 ![]() cm/s���ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��4cm/s���ٶ����B�ƶ�������R�ӵ�B��ʼ��BO��2cm/s���ٶ����O�ƶ������P��Q��R�ֱ��O��A��Bͬʱ�ƶ����ƶ�ʱ��Ϊt��0��t��6��s��
cm/s���ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��4cm/s���ٶ����B�ƶ�������R�ӵ�B��ʼ��BO��2cm/s���ٶ����O�ƶ������P��Q��R�ֱ��O��A��Bͬʱ�ƶ����ƶ�ʱ��Ϊt��0��t��6��s�� 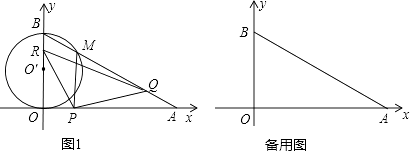
��1�����OAB�Ķ�����
��2����OBΪֱ���ġ�O����AB���ڵ�M����tΪ��ֵʱ��PM���O�����У�
��3���Ƿ���ڡ�RPQΪ���������Σ������ڣ���ֱ��д��tֵ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��Rt��AOB�У�
tan��OAB= ![]() =
= ![]() =
= ![]() ��
��
���OAB=30��
��2���⣺��ͼ������O��P��O��M��
��PM���O������ʱ���У�
��PMO��=��POO��=90�㣬
��PMO��ա�POO�䣮
�ɣ�1��֪��OBA=60�㣬
��O��M=O��B��
���O��BM�ǵȱ������Σ�
���BO��M=60�㣮
�ɵá�OO��P=��MO��P=60�㣮
��OP=OO��tan��OO��P
=6��tan60��=6 ![]() ��
��
�֡�OP=2 ![]() t��
t��
��2 ![]() t=6
t=6 ![]() ��t=3��
��t=3��
����t=3ʱ��PM���O������
��3���⣺���ڡ�RPQΪ���������Σ�
�������£��������֪��PR2=16t2��48t��PQ2=52t2��288t��RQ2=28t2��240t+576��
����PR=RQʱ���ɵ�t=8��2 ![]() ��t=8+
��t=8+ ![]() ��ȥ����
��ȥ����
����PR=PQʱ���ɵ�t= ![]() ��
��
����RQ=PQʱ���ɵ�t=1+ ![]() ��t=1��
��t=1�� ![]() ��ȥ��
��ȥ��
���Ͽ�֪����t=8��2 ![]() ��
�� ![]() ��1+
��1+ ![]() ʱ����RPQΪ���������Σ�
ʱ����RPQΪ���������Σ�
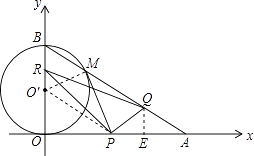
����������1����Rt��OAB�У���֪��OA��OB�ij������������OAB������ֵ���ɴ˿ɵõ���OAB�Ķ�������2������O��M����PM���O������ʱ��PM��POͬΪ��O������ߣ���֤�á�OO��P�ա�MO��P�����OO��P=��MO��P���ڣ�1�����á�OBA=60�㣬����O��BM�ǵȱ������Σ��ɴ˿ɵõ���BO��M=��PO��M=��PO��O=60�㣻��Rt��OPO���У����ݡ�PO��O�Ķ�����OO��ij��������OP�ij�����֪��P����˶��ٶȣ����ɸ���ʱ��=·�̡��ٶ����t��ֵ����3�����ڡ�RPQΪ���������Σ����ڡ�QPQ�����͵ײ�ȷ������������ۣ���PR=RQ����PR=PQ����RQ=PQʱ�ֱ�������������tֵ���ɣ�