题目内容
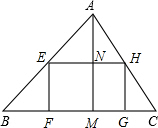
在底边长BC=20cm，高AM=12cm的三角形铁板ABC上，要截一块矩形铁板EFGH，如图所示，当矩形的边EF=______时，矩形铁板的面积最大，其最大面积为______cm2．
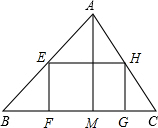
如图，设矩形EFGH的宽EF=x，则AN=AM-MN=12-x，
∵矩形的对边EH∥FG，
∴△AEH∽△ABC，
∴
=
，
即
=
，
解得：EH=
，
四边形EFGH的面积=x×
=-
x2+20x=-
（x-6）2+60，
所以，当x=6，即EF=6时，四边形EFGH最大面积为60cm2．
故答案为：6、60．
∵矩形的对边EH∥FG，
∴△AEH∽△ABC，
∴
| AN |
| AM |
| EH |
| BC |
即
| 12-x |
| 12 |
| EH |
| 20 |
解得：EH=
| 60-5x |
| 3 |
四边形EFGH的面积=x×
| 60-5x |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
所以，当x=6，即EF=6时，四边形EFGH最大面积为60cm2．
故答案为：6、60．
练习册系列答案
相关题目
米的黄丽同学BC的影长BA为1.1米，与此同时，测得教学楼DE的影长DF为12.1米．
