题目内容
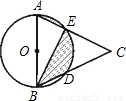
(2005•深圳)如图,?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的F点,若△FDE的周长为8 cm,△FCB的周长为20cm,则FC的长为 cm.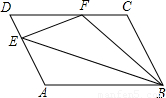
【答案】分析:根据折叠的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
解答:解:AE=EF,AB=BF;△FDE的周长为DE+FE+DF=AD+DF=8cm,△FCB的周长为FC+AD+AB=20 cm,
分析可得:FC= [FC+AD+AB-(AD+DF)]=
[FC+AD+AB-(AD+DF)]= (2FC)=
(2FC)= (△FCB的周长-△FDE的周长)=
(△FCB的周长-△FDE的周长)= (20-8)=6cm.
(20-8)=6cm.
故答案为6.
点评:本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.
解答:解:AE=EF,AB=BF;△FDE的周长为DE+FE+DF=AD+DF=8cm,△FCB的周长为FC+AD+AB=20 cm,
分析可得:FC=
 [FC+AD+AB-(AD+DF)]=
[FC+AD+AB-(AD+DF)]= (2FC)=
(2FC)= (△FCB的周长-△FDE的周长)=
(△FCB的周长-△FDE的周长)= (20-8)=6cm.
(20-8)=6cm.故答案为6.
点评:本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 π-
π-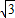
 π
π π-
π-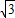
 π
π
 π-
π-
 π
π π-
π-
 π
π